Lingxiao Zhang

Biography: Lingxiao Zhang is an Assistant Research Professor in the Department of Mathematics at the University of Connecticut. She completed her Ph.D. at the University of Wisconsin-Madison under the supervision of Brian Street. Her research focuses on harmonic analysis, linear and multilinear singular integrals, sub-Riemannian geometry, several complex variables, and spectral multipliers of partial differential equations.
Title: Bounded singular Radon transforms
Abstract: We discuss the Lp boundedness of singular Radon transforms, including real analytic singular Radon transforms with product kernels, Hilbert transforms along flat curves in the Heisenberg group, and singular integrals along C1,α graphs or regular curves in the Heisenberg group. We will use some examples to illustrate the conditions for Lp boundedness in different scenarios and discuss the difficulties in precisely characterizing all bounded singular Radon transforms.
Lidia Mrad

Biography: Lidia Mrad is an Assistant Professor in the Department of Mathematics at Mount Holyoke College. Before coming to Mount Holyoke College, she earned her Ph.D. at Purdue University under the supervision of Daniel Phillips, and completed a postdoc at the University of Arizona under the mentorship Joceline Lega. Her research focuses on solving problems, analytically and/or computationally, arising from physical setups such as those describing liquid crystals, population growth patterns, or epidemiology. The techniques she uses belong to the areas of partial differential equations, the calculus of variations, agent-based modeling, and numerical simulations.
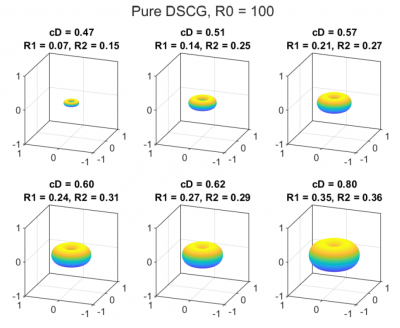
Title: Aggregation in chromonic liquid crystals
Abstract: Liquid crystals are materials that can flow like liquids, but their molecules are usually oriented in a common direction like crystalline solids. In addition to being partially ordered, chromonic liquid crystals manifest sensitivity to changes in concentration when added to a solution. Their disc-like molecules tend to form rings when their concentration reaches a threshold value. These rings then aggregate into interesting geometrical shapes. We study how key parameters affect toroidal shape formation by formulating the question as a constrained energy minimization problem. Specifically, we show when a torus solution to the ensuing equation exists and compute its dimensions. Our optimal torus sizes match closely those obtained from experiments with DSCG, a drug used to treat asthma. These results can also shed light on the packing mechanism of a viral DNA in a capsid, since confined DNA forms chromonic liquid crystal phases.